Advertisements
Advertisements
प्रश्न
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
उत्तर
Let a m be the side of the square.
Area of the square
= a2
Thus, we have :
a2 = 1600
⇒ a = 40
Area of the plots = 4(Area of the semicircle of radius 20 m)
`=|4(1/2pi"r"^2)"m"^2|`
`=|4(1/2xx3.14xx20xx20)|"m"^2`
= 2512 m2
∴ Cost of turfing plots at 12.50 per m2 = Rs (2512 × 12.50)
= Rs 31400
APPEARS IN
संबंधित प्रश्न
The length and breadth of a rectangular garden are in the ratio 9:5. A path 3.5 m wide, running all around inside it has an area of `1911m^2` . Find the dimensions of the garden.
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
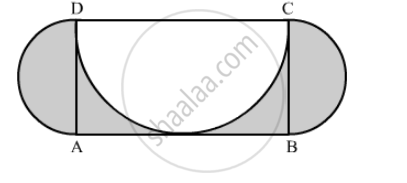
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
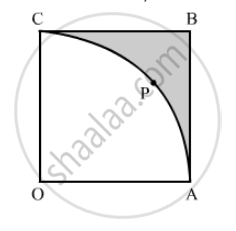
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
If he area of a sector of a circle is \[\frac{7}{20}\] of the area of the circle, then the sector angle is equal to
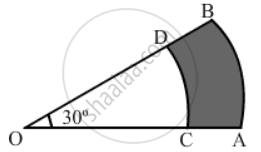
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
Two circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres us 10cm. Find the radii of the two circles.
Calculate the area of the shotput circle whose radius is 2.135 m.
