Advertisements
Advertisements
प्रश्न
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
उत्तर
n 2 days, the short hand will complete 4 rounds.
Length of the short hand = 4 cm
Distance covered by the short hand = 4 × 2π × 6 = 576 π cm
In the same 2 days, the long hand will complete 48 rounds.
Length of the long hand = 6 cm
Distance covered by the long hand = 48 × π × 6 = 576π cm
∴ Total distance covered by the hands = Distance covered by the short hand + Distance covered by the long hand
= 32π + 576π
= 608 π
= 608 × 3.14
= 1909.12 cm
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
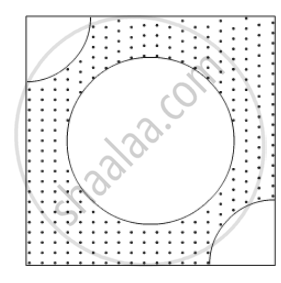
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
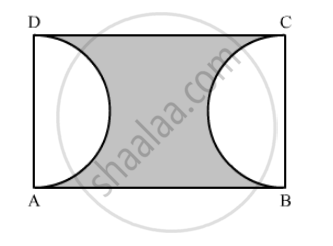
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
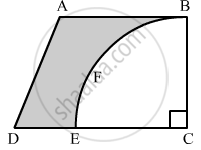
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area the circle.
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
