Advertisements
Advertisements
प्रश्न
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).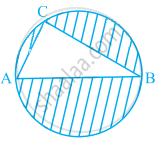
उत्तर
Given, AC = 6 cm and BC = 8 cm
We know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.
∴ ∠C = 90°
In right angled ΔACB, use Pythagoras theorem,
∴ AB2 = AC2 + CB2
⇒ AB2 = 62 + 82
⇒ AB2 = 36 + 64
⇒ AB2 = 100
⇒ AB = 10 cm ...[Since, side cannot be negative]
∴ Area of ΔABC = `1/2 xx "BC" xx "AC"`
= `1/2 xx 8 xx 6`
= 24 cm2
Here, diameter of circle,
AB = 10 cm
∴ Radius of circle,
r = `10/2` = 5 cm
Area of circle = πr2
= 3.14 × (5)2
= 3.14 × 25
= 78.5 cm2
∴ Area of the shaded region = Area of circle – Area of ΔABC
= 78.5 – 24
= 54.5 cm2
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
Lalitha wants to buy a round carpet of radius is 63 cm for her hall. Find the area that will be covered by the carpet
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
