Advertisements
Advertisements
प्रश्न
If the circumference and the area of a circle are numerically equal, then diameter of the circle is
विकल्प
\[\frac{\pi}{2}\]
2\[\frac{\pi}{2}\]
2
4
उत्तर
We have given that circumference and area of a circle are numerically equal.
Let it be x.
Let r be the radius of the circle, therefore, circumference of the circle is `2pir`and area of the circle will be `pir^2`.
Therefore, from the given condition we have,
`2pir=x .................(1)`
`pi r^2 = x ...............(2)`
Therefore, from equation (1) get `r=x/(2pi)`. Now we will substitute this value in equation
we get, `pi(x/(2pi))^2=x`
Simplifying further we get,
`pixx x^2/(4pi^2)=x`
Cancelling x we get,
`pi xx x/(4pi^2)=1`
Now we will cancel `pi`
`x/(4pi)=1...........(3)`
Now we will multiply both sides of the equation (3) by `4pi` we get, `x=4pi`
We can rewrite this equation as given below, `x=2xxpixx2`
Comparing equation (4) with equation (1) we get r = 2.
Therefore, radius of the circle is 2. We know that diameter of the circle is twice the radius of the circle.
`∴ "diameter"=2xx "radius"`
`∴ "diameter"=2xx2`
`∴"diameter"=4`
Therefore, diameter of the circle is 4.
Hence, option (d) is correct.
APPEARS IN
संबंधित प्रश्न
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/m2. (Take π = 3.14)
The perimeter of a rectangular plot of land is 80 m and its breadth is 16 m. Find the length and area of the plot.
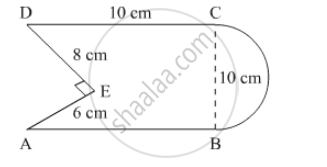
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
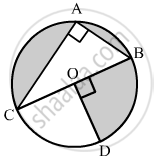
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
