Advertisements
Advertisements
Question
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).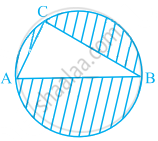
Solution
Given, AC = 6 cm and BC = 8 cm
We know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.
∴ ∠C = 90°
In right angled ΔACB, use Pythagoras theorem,
∴ AB2 = AC2 + CB2
⇒ AB2 = 62 + 82
⇒ AB2 = 36 + 64
⇒ AB2 = 100
⇒ AB = 10 cm ...[Since, side cannot be negative]
∴ Area of ΔABC = `1/2 xx "BC" xx "AC"`
= `1/2 xx 8 xx 6`
= 24 cm2
Here, diameter of circle,
AB = 10 cm
∴ Radius of circle,
r = `10/2` = 5 cm
Area of circle = πr2
= 3.14 × (5)2
= 3.14 × 25
= 78.5 cm2
∴ Area of the shaded region = Area of circle – Area of ΔABC
= 78.5 – 24
= 54.5 cm2
APPEARS IN
RELATED QUESTIONS
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
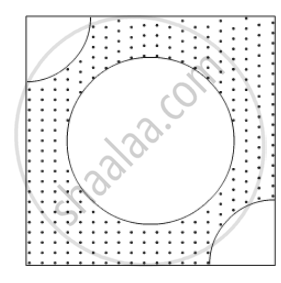
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
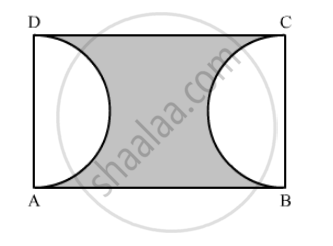
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
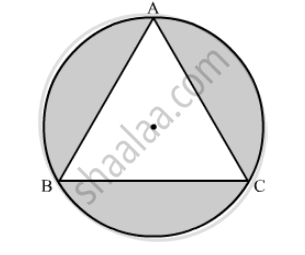
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
In the following figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π =3.142 and`sqrt3` = 1.732).

Find the area of sector of circle of radius 21 cm and central angle 1200.
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
The area of a sector whose perimeter is four times its radius r units, is
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centers is 12 cm. Find the diameters of the circle.
