Advertisements
Advertisements
प्रश्न
The area of a sector whose perimeter is four times its radius r units, is
पर्याय
\[\frac{r^2}{4}\]
2r2 sq. units
r2 sq.units
उत्तर
We know that perimeter of the sector= `2r+θ/360xx2pir`
We have given that perimeter of the sector is four times the radius.
`2r+θ/360x2pir=4r`
Subtracting 2r from both sides of the equation,
`∴ θ/360xx2pir^=4r-2r`
`∴ θ/360xx2pir=2r`
Dividing both sides of the equation 2r we get,
`θ/360=pi=1`
`∴ θpi/360=1`.............(1)
Let us find the area of the sector.
∴ Area of the sector=`θ/360 pir^2`
Substituting `θpi/360=1` we get,
Area of the sector=`r^2`
Hence, area of the sector is `r^2 `sq.units
APPEARS IN
संबंधित प्रश्न
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

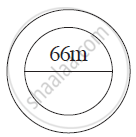
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
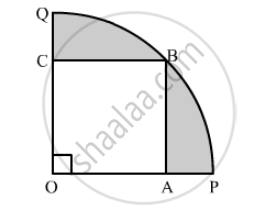
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
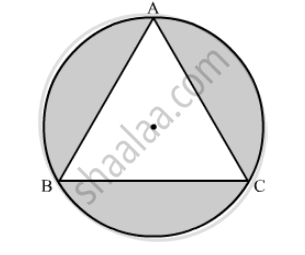
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park.
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
The area of a sector of a circle with radius r, making an angle of x° at the centre is
The area (in cm2) of the circle that can be inscribed in a square of side 8 cm is ____________.
