Advertisements
Advertisements
प्रश्न
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
उत्तर
We know that the area of minor segment of angle θ in a circle of radius r is,
`A={(piθ)/360°-sin θ/2 cos θ/2}r^2`
It is given that the chord PQ divides the circle in two segments.
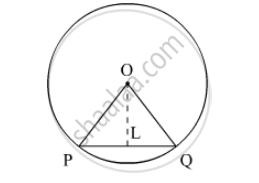
We have ∠POQ=120° and`PQ=12 cm`. So,
`PL=(PQ)/2 cm`
`=12/2 cm`
`= 6 cm`
Since `∠POQ=120°`
`∠POL=∠QOL`
`=60°`
In ΔOPQ, We have
`sin θ=(PL)/(OA)`
`sin 60°=6/(OA)`
`sqrt3/2=6/(OA)`
`OA=12/sqrt3`
Thus the radius of circle is `OA=4sqrt3 cm`
Now using the value of radius r and angle θ we will find the area of minor segment
`A={(120°pi)/(360°)-sin (120°)/2 cos (120°)/2} (4sqrt3)^2`
`= {pi/3-sqrt3/2xx1/2}xx48`
`= 4{4pi-3sqrt3}cm^2`
APPEARS IN
संबंधित प्रश्न
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The perimeter of the sector OAB shown in the following figure, is

If diameter of a circle is increased by 40%, then its area increase by
The area of a sector whose perimeter is four times its radius r units, is
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
The diameter of the wheels of a bus is 140 cm. How many revolutions per minute do the wheels make when the bus is moving at a speed of 72.6 km per hour?
The ratio of the area of a circle to the area of its semicircle is
In figure, AB is a diameter of the circle, AC = 6 cm and BC = 8 cm. Find the area of the shaded region (Use π = 3.14).