Advertisements
Advertisements
Question
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
Solution
We know that the area of minor segment of angle θ in a circle of radius r is,
`A={(piθ)/360°-sin θ/2 cos θ/2}r^2`
It is given that the chord PQ divides the circle in two segments.
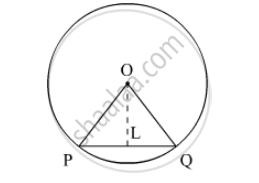
We have ∠POQ=120° and`PQ=12 cm`. So,
`PL=(PQ)/2 cm`
`=12/2 cm`
`= 6 cm`
Since `∠POQ=120°`
`∠POL=∠QOL`
`=60°`
In ΔOPQ, We have
`sin θ=(PL)/(OA)`
`sin 60°=6/(OA)`
`sqrt3/2=6/(OA)`
`OA=12/sqrt3`
Thus the radius of circle is `OA=4sqrt3 cm`
Now using the value of radius r and angle θ we will find the area of minor segment
`A={(120°pi)/(360°)-sin (120°)/2 cos (120°)/2} (4sqrt3)^2`
`= {pi/3-sqrt3/2xx1/2}xx48`
`= 4{4pi-3sqrt3}cm^2`
APPEARS IN
RELATED QUESTIONS
Find the area of the circle in which a square of area 64 cm2 is inscribed. [Use π = 3.14]
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
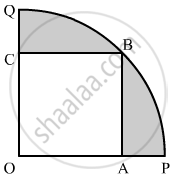
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
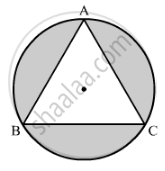
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
The circumference of a circular park is 352 m. Find the area of the park
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
If the radius of a circle is tripled, the area becomes ______.
