Advertisements
Advertisements
Question
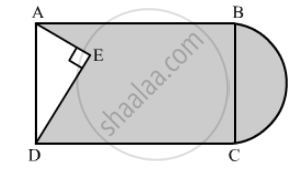
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
Solution
In right triangle AED
AD2 = AE2 + DE2
= (9)2 + (12)2
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC = 15 cm
Area of the shaded region = Area of rectangle − Area of triangle AED + Area of semicircle
\[= AB \times BC - \frac{1}{2} \times AE \times DE + \frac{1}{2}\pi \left( \frac{BC}{2} \right)^2 \]
\[ = 20 \times 15 - \frac{1}{2} \times 9 \times 12 + \frac{1}{2} \times \frac{22}{7} \times \left( \frac{15}{2} \right)^2 \]
\[ = 300 - 54 + 88 . 3928\]
\[ = 334 . 3928 {cm}^2\]
Hence, the area of shaded region is 334.39 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 600 .
If the radius of a circle is diminished by 10%, then its area is diminished by
The perimeter of the sector OAB shown in the following figure, is

The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
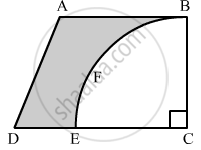
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
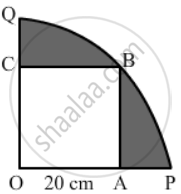
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
Find the area of a circle of radius 30 cm (use π = 3.14).
Area of a circle with diameter ‘m’ radius ‘n’ and circumference ‘p’ is ______.
