Advertisements
Advertisements
प्रश्न
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)

उत्तर
Perimeter of the shaded portion = 4 ⨯ Length of the arc having central angle 90∘
\[= 4 \times \frac{90°}{360°} \times 2 \times \frac{22}{7} \times \frac{14}{2}\]
\[ = 4 \times \frac{1}{4} \times 2 \times \frac{22}{7} \times 7\]
\[ = 44 cm\]
Area of shaded portion = Area of square ABCD − 4 ⨯ Area of the arc having central angle 90∘
\[= \left( 14 \right)^2 - 4 \times \frac{90°}{360°} \times \frac{22}{7} \times \left( \frac{14}{2} \right)^2 \]
\[ = 196 - 4 \times \frac{1}{4} \times \frac{22}{7} \times \left( 7 \right)^2 \]
\[ = 196 - 154\]
\[ = 42 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. (Use π = `22/7`)
Find the area of the shaded region in the following figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)
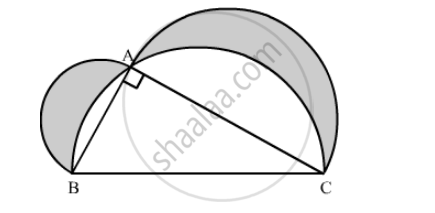
In the following figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.
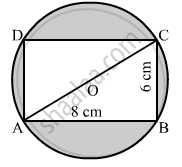
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
The length of an arc of a circle, subtending an angle of 54° at the centre, is 16.5 cm. Calculate the radius, circumference and area of the circle.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.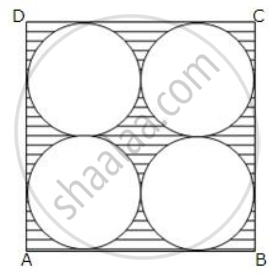
Find the area of the remaining card-board.
The radii of two circles are in the ratio 5 : 8. If the difference between their areas is 156p cm2, find the area of the bigger circle.
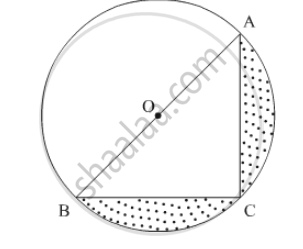
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
