Advertisements
Advertisements
प्रश्न
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
उत्तर
Let AB be the diameter of the semi-circular protractor.
So, `AB=14 cm`
`"We know that perimeter of the semicircle" = 1/2 (2pi r)+2r .........(1)`
We have given the diameter of the protractor.
Therefore, radius of the protractor =`14/2`
So, radius of the protractor `=7`
Substituting the value of r in equation (1) we get,
Perimeter of the semi-circular protractor=`1/2(2pxx7)+2xx7`
Perimeter of the semi-circular protractor=`(pixx7)+14`
Substituting `pi=22/7` we get
`"Perimeter of the semi-circular protractor"=(22/7xx7)+14`
`"Perimeter of the semi-circular protractor"=22+14`
`"Hence Perimeter of the semi-circular protractor"'=36`
Therefore, perimeter of the semi-circular protractor is ` 36 cm`
APPEARS IN
संबंधित प्रश्न
A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is `3375m^2` . Find the cost of fencing the lawn at ₹ 65 per metre.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
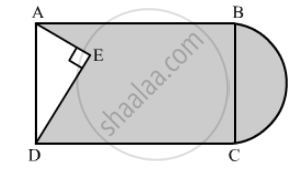
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
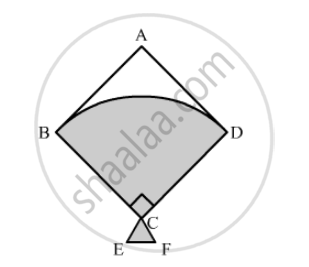
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
ABCD is a rectangle whose three vertices are B (4,0), C (4,3) and D (0, 3). The length of one of its diagonals is
Find the area of a ring whose outer and inner radii are respectively 23 cm and 12 cm.
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
