Advertisements
Advertisements
प्रश्न
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
उत्तर
Let r1 and r2 be the radii of two circles.
⇒ r1 + r2 = 10.5 ....(i)
And,
`2π"r"_(6.3-4.21) - 2π"r"_2` = 13.2
⇒ `2 xx (22)/(7) xx ("r"_1 - "r"_2)` = 13.2
⇒ r1 - r2 = `(13.2 xx 7)/(2 xx 22)`
⇒ r1 - r2 = 2.1 ....(ii)
Adding (i) and (ii), we get
2r1 = 12.6
⇒ r1 = 6.3cm
Now,
r1 - r2 = 2.1
⇒ 6.3 - r2 = 2.1
⇒ r2 = 4.2cm.
APPEARS IN
संबंधित प्रश्न
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
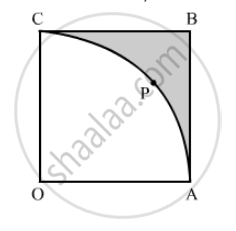
In the following figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region. (Use π = 22/7)
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
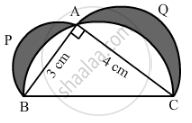
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The diameters of three circles are in the ratio 3: 5: 6. If the sum of the circumferences of these circles is 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Calculate the area of the shotput circle whose radius is 2.135 m.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
