Advertisements
Advertisements
Question
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
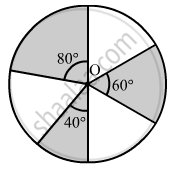
Solution
Area of the shaded region = Area of sector having central angle 60∘ + Area of sector having central angle 80∘ + Area of sector having central angle 40∘
`=["60°"/"360"^circ]xxpi(7)^2 + [80^circ/360^circ] + [80^circ/360^circ xx pi(7)^2]+[40^circxxpi(7)^2]`
`=pi(7)^2 (60^circ/360^circ + 80^circ/360^circ+40^circ/360^circ)`
`=pi(7)^2(1/2)`
= 77 cm2
Hence, the area of the shaded region is 77 cm2 .
APPEARS IN
RELATED QUESTIONS
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
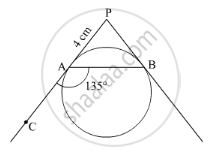
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
The area of the sector of a circle with radius 6 cm and of angle 60° is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
