Advertisements
Advertisements
प्रश्न
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
पर्याय
True
False
उत्तर
This statement is False.
Explanation:
It is true for arcs of the same circle.
But in different circle, it is not possible.
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
Find the area of the sector whose arc length and radius are 8 cm and 3 cm respectively.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.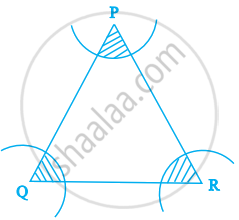
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
