Advertisements
Advertisements
प्रश्न
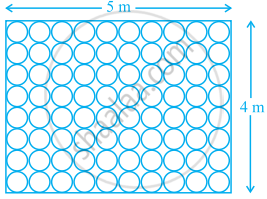
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
उत्तर
Given, floor of a room is covered with circular tiles.
Length of a floor of a room (l) = 5 m
And breadth of floor of a room (b) = 4 m
∴ Area of floor of a room = l × b
= 5 × 4
= 20 m2
⇒ Radius of each circular tile (r) = `50/2 "cm"`
= 25 m
= `25/100 "m"`
= `1/4 "m"`
Now, area of a circular tile = πr2
= `3.14 xx (1/4)^2 "m"^2`
= `3.14/16 "m"^2`
∴ Number of circular tiles = 80
∴ Area of 80 circular tiles
= `80 xx 3.14/16`
= 5 × 3.14
= 15.7 m2
So, area of floor that remains uncovered with tiles = Area of floor of a room – Area of 80 circular tiles
= 20 – 15.7
= 4.3 m2
Hence, the required area of floor that remains uncovered with tiles is 4.3 m2.
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC an BSD are semicircles of diameter 14 cm each. Find the
- perimeter
- area of the shaded region.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Find the difference of the areas of a sector of angle 120° and its corresponding major sector of a circle of radius 21 cm.
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.