Advertisements
Advertisements
प्रश्न
Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
उत्तर
Here, M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
We have to prove that
∠BMN = ∠CNM
∠AMN = ∠DNM
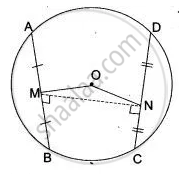
Join ON, OM and NM
∴ ∠OMA = ∠OMB = 90°
∠ OND = ∠ONC = 90° ....(i)(Line joining the centre and midpoint of a chord is perpendicular to the chord)
Since, AB = CD ⇒ OM = ON
∴ In ΔOMN, ∠OMN = ∠ONM ...(ii)
(i) ∠OMB = ∠ONC ...[ Using (i) and (ii) ]
∠OMN = ∠ONM
⇒ ∠OMB - ∠OMN = ∠ONC - ∠ONM
⇒ ∠BMN = ∠CNM
(ii) ∠OMA = ∠OND
∠OMN = ∠ONM ...[ Using (i) and (ii) ]
⇒ ∠OMA + ∠OMN = ∠OND + ∠ONM
⇒ ∠AMN = ∠DNM
Hence proved.
APPEARS IN
संबंधित प्रश्न
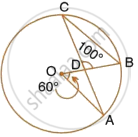
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
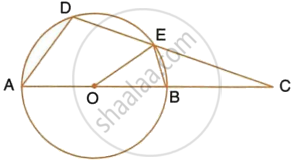
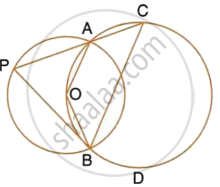
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
- ∠AOB,
- ∠ACB,
- ∠ABD,
- ∠ADB.
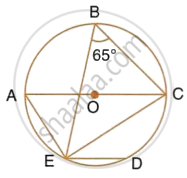
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
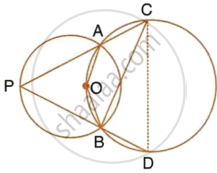
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
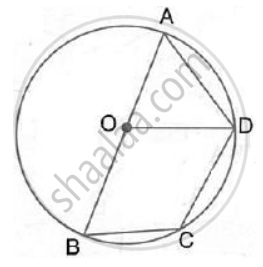
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ACB

In the given Figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is the radius of the circumcircle of A ABC, whose center is O.
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
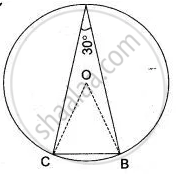
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = x° and ∠AOB = y° express y in terms of x. Calculate x, if ACBO is a parallelogram.
