Advertisements
Advertisements
प्रश्न
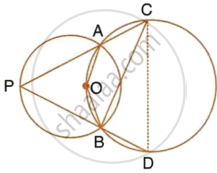
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
- ∠AOB,
- ∠ACB,
- ∠ABD,
- ∠ADB.
उत्तर
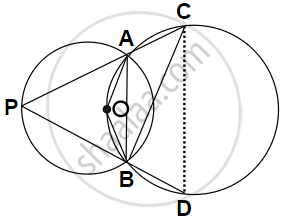
Join AB and AD
i. ∠AOB = 2∠APB
= 2 × 75°
= 150°
(Angle at the centre is double the angle at the circumference subtended by the same chord).
ii. In cyclic quadrilateral AOBC,
∠ACB = 180° – ∠AOB
= 180° – 150°
= 30°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
iii. In cyclic quadrilateral ABDC
∠ABD = 180° – ∠ACD
= 180° – (40° + 30°)
= 110°
(Pair of opposite angles in a cyclic quadrilateral are supplementary
iv. In cyclic quadrilateral AOBD,
∠ADB = 180° – ∠AOB
= 180° – 150°
= 30°
(Pair of opposite angles in a cyclic quadrilateral are supplementary
APPEARS IN
संबंधित प्रश्न
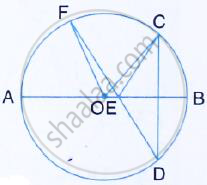
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
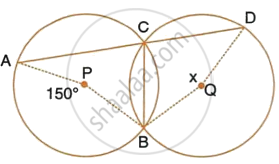
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

In the given figure, AB is the diameter of the circle with centre O.
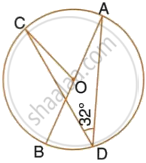
If ∠ADC = 32°, find angle BOC.
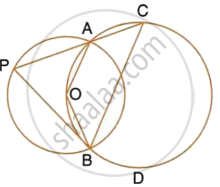
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
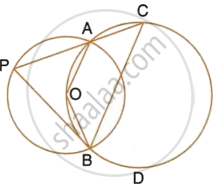
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ADB.
Give reasons for your answers clearly.
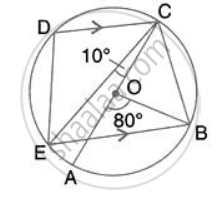
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate : Angle BCD
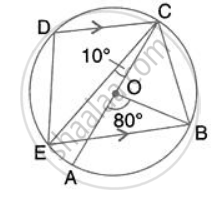
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
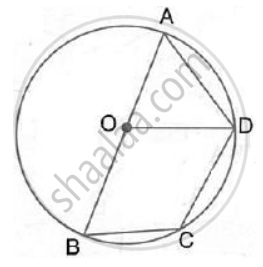
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

