Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter of the circle with centre O.
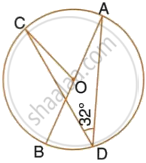
If ∠ADC = 32°, find angle BOC.
उत्तर
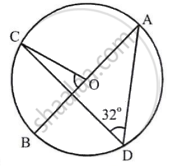
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠ADC
`=>` ∠AOC = 2 × 32° = 64°
Since ∠AOC and ∠BOC are linear pair, we have
∠AOC + ∠BOC = 180°
`=>` 64° + ∠BOC = 180°
`=>` ∠BOC = 180°
`=>` ∠BOC = 180° – 64°
`=>` ∠BOC = 116°
APPEARS IN
संबंधित प्रश्न
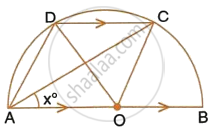
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :
- ∠COB,
- ∠DOC,
- ∠DAC,
- ∠ADC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
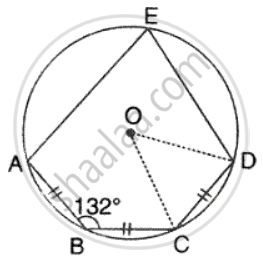
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

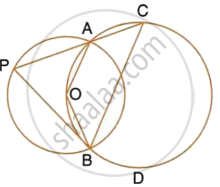
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
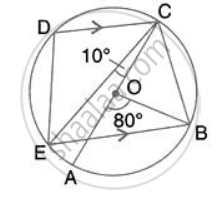
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ACB

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.
Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
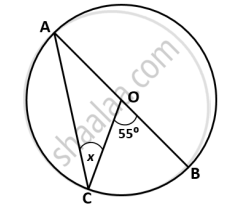
In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠COB = 55⁰ then the value of x is: