Advertisements
Advertisements
प्रश्न
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
उत्तर
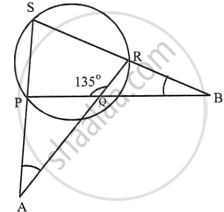
PQRS is a cyclic quadrilateral in which ∠PQR = 135°
Sides SP and RQ are produced to meet at A and sides PQ and SR are produced to meet at B.
∠A : ∠B = 2 : 1
Let ∠A = 2x, then ∠B = x
Now, in cyclic quad PQRS,
Since, ∠PQR = 135°, ∠S = 180° – 135° = 45°
[Since sum of opposite angles of a cyclic quadrilateral are supplementary]
Since, ∠PQR and ∠PQA are linear pair,
∠PQR + ∠PQA = 180°
`=>` 135° + ∠PQA = 180°
`=>` ∠PQA = 180° – 135° = 45°
Now, In ∆PBS,
∠P = 180° – (45° + x)
= 180° – 45° – x
= 135° – x ...(1)
Again, in ∆PQA,
EXT ∠P = ∠PQA + ∠A
= 45° + 2x ...(2)
From (1) and (2),
45° + 2x = 135° – x
`=>` 2x + x = 135° – 45°
`=>` 3x = 90°
`=>` x = 30°
Hence, ∠A = 2x = 2 × 30° = 60° and ∠B = x = 30°
APPEARS IN
संबंधित प्रश्न
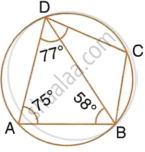
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
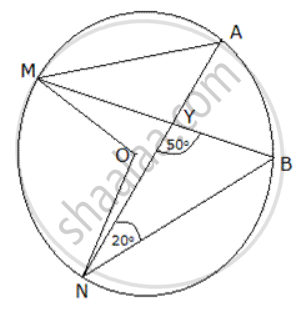
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
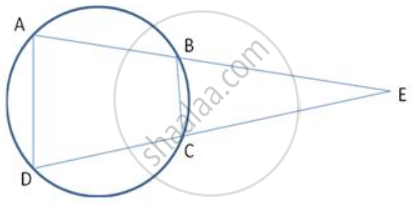
In the figure, given below, find: ∠ADC, Show steps of your working.
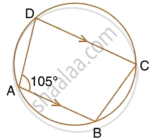
In the following figure, Prove that AD is parallel to FE.

