Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter of the circle with centre O.
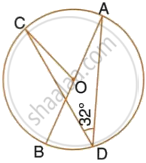
If ∠ADC = 32°, find angle BOC.
उत्तर
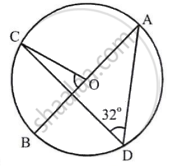
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠ADC
`=>` ∠AOC = 2 × 32° = 64°
Since ∠AOC and ∠BOC are linear pair, we have
∠AOC + ∠BOC = 180°
`=>` 64° + ∠BOC = 180°
`=>` ∠BOC = 180°
`=>` ∠BOC = 180° – 64°
`=>` ∠BOC = 116°
APPEARS IN
संबंधित प्रश्न
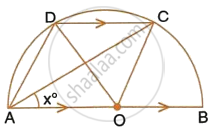
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :
- ∠COB,
- ∠DOC,
- ∠DAC,
- ∠ADC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
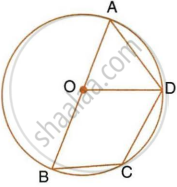
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

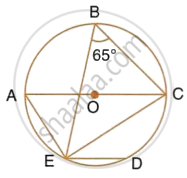
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
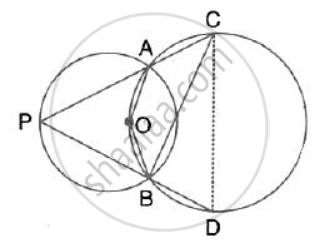
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ACB

In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ABD
In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.
In the given Figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is the radius of the circumcircle of A ABC, whose center is O.
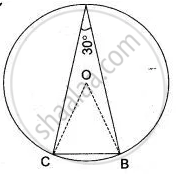
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = x° and ∠AOB = y° express y in terms of x. Calculate x, if ACBO is a parallelogram.
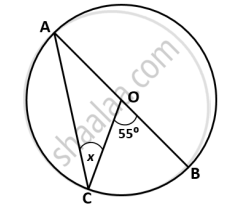
In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠COB = 55⁰ then the value of x is: