Advertisements
Advertisements
प्रश्न
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

उत्तर
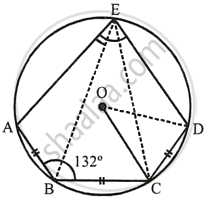
In the figure, O is the centre of circle, with AB = BC = CD.
∠ABC = 132°
i. In cyclic quadrilateral ABCE
∠ABC + ∠AEC = 180° ...[Sum of opposite angles]
`=>` ∠132° + ∠AEC = 180°
`=>` ∠AEC = 180° – 132°
`=>` ∠AEC = 48°
Since, AB = BC, ∠AEB = ∠BEC ...[Equal chords subtends equal angles]
∴ `∠AEB = 1 /2 ∠AEC`
= `1/2 xx 48^circ`
= 24°
ii. Similarly, AB = BC = CD
∠AEB = ∠BEC = ∠CED = 24°
∠AED = ∠AEB + ∠BEC + ∠CED
= 24° + 24° + 24°
= 72°
iii. Arc CD subtends ∠COD at the centre and ∠CED at the remaining part of the circle.
∴ COD = 2∠CED
= 2 × 24°
= 48°
APPEARS IN
संबंधित प्रश्न
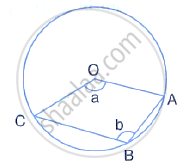
The figure given below, shows a Circle with centre O.
Given: ∠AOC = a and ∠ABC = b.
Find the relationship between a and b
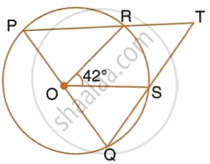
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
- ∠AOB,
- ∠ACB,
- ∠ABD,
- ∠ADB.
In the given figure, AB is the diameter of the circle with centre O.
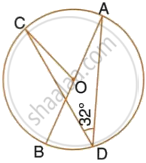
If ∠ADC = 32°, find angle BOC.
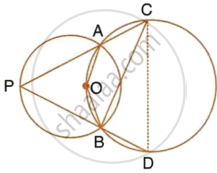
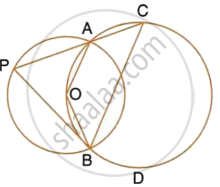
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
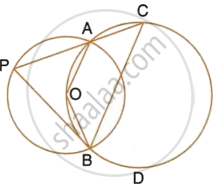
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ADB.
Give reasons for your answers clearly.
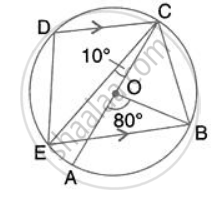
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate : Angle BCD
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ACB

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠AED

C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = x° and ∠AOB = y° express y in terms of x. Calculate x, if ACBO is a parallelogram.
