Advertisements
Advertisements
प्रश्न
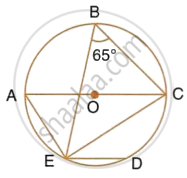
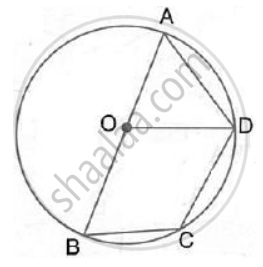
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
उत्तर
Join OE,
Arc EC subtends ∠EOC at the centre and ∠EBC at the remaining part of the circle.
∠EOC = 2∠EBC = 2 × 65° = 130°
Now in ΔOEC, OE = OC ...[Radii of the same circle]
∴ ∠OEC = ∠OCE
But, in ΔEOC,
∠OEC + ∠OCE + ∠EOC = 180° ...[Angles of a triangle]
`=>` ∠OCE + ∠OCE + ∠EOC = 180°
`=>` 2∠OCE + 130° = 180°
`=>` 2∠OCE = 180° – 130°
`=>` 2∠OCE = 50°
`=> ∠OCE = 50^circ/2 = 25^circ`
∴ AC || ED ...[Given]
∴ ∠DEC = ∠OCE
`=>` ∠DEC = 25°
APPEARS IN
संबंधित प्रश्न
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
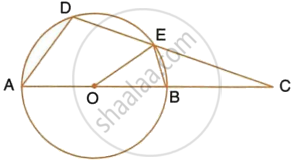
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angle ADC.
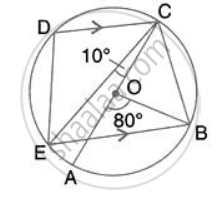
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate : Angle BCD
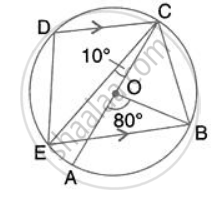
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
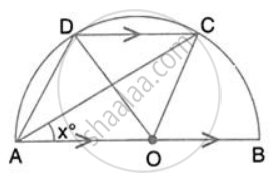
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DAC
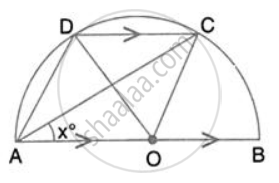
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ ADC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
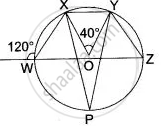
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.