Advertisements
Advertisements
Question
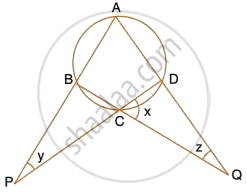
Calculate the angles x, y and z if :
`x/3 = y/4 = z/5`
Solution
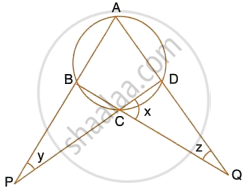
Let x = 3k, y = 4k and z = 5k
∠ADC = x + z = 8k and ∠ABC = x + y = 7k
(Exterior angle of a ∆ is equal to the sum of pair of interior opposite angles)
Also, ∠ABC + ∠ADC = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 8k + 7k = 180°
`=>` 15k = 180°
∴ `k = 180^circ/15 = 12^circ`
∴ x = 3 × 12° = 36°
y = 4 × 12° = 48°
z = 5 × 12° = 60°
APPEARS IN
RELATED QUESTIONS
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.
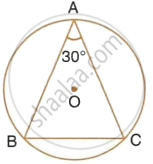
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
- angle QTR
- angle QRP
- angle QRS
- angle STR
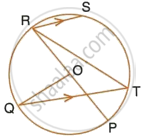
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(ii) angle QRP

The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iii) angle QRS
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iv) angle STR

In the given figure, an equilateral triangle ABC is inscribed in a circle with center O.
Find: (i) ∠BOC
(ii) ∠OBC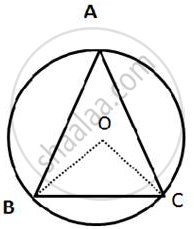
In the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight-sided polygon.
Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC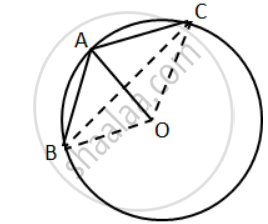
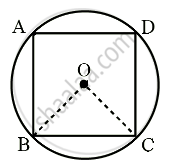
In the given figure, a square is inscribed in a circle with center O. Find:
- ∠BOC
- ∠OCB
- ∠COD
- ∠BOD
Is BD a diameter of the circle?
In the given figure, arc AB and arc BC are equal in length. If ∠AOB = 48°, find:
(i) ∠BOC
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠OAC