Advertisements
Advertisements
Question
In the given figure, a square is inscribed in a circle with center O. Find:
- ∠BOC
- ∠OCB
- ∠COD
- ∠BOD
Is BD a diameter of the circle?
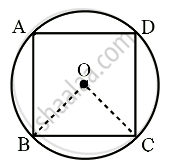
Solution 1
In the given figure we can extend the straight line OB to BD and CO to CA
Then we get the diagonals of the square which intersect each other at 90 by the property of Square.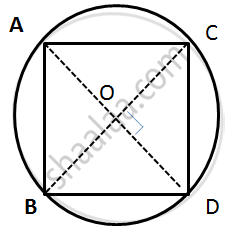
From the above statement, we can see that
∠COD = 90°
The sum of the angle ∠BOC and ∠COD is 180° as BD is a straight line.
Hence ∠BOC + ∠OCD = ∠BOD = 180°
∠BOC + 90° = 180°
∠BOC + 180° - 90°
∠BOC = 90°
We can see that the OCB is an isosceles triangle with sides OB and OC of EQual length as they are the radii of the same are.
In ΔOCB,
∠OBC = ∠OCB as they are opposite angles to the two equal sides of an isosceles triangle.
Sum of all the angles of a triangle is 180°
so, ∠OBC + ∠OCB + ∠BOC =180°
∠OBC + ∠OBC + 90° = 180° as, ∠OBC = ∠OCB
2∠OBC = 180° - 90°
2∠OBC = 90°
2∠OBC = 45°
as ∠OBC = ∠OCB So,
∠OBC = OCB = 45°
Yes BD is the diameter of the order.
Solution 2
From the figure, extend a straight-line OB to BD and CO to CA.
We get the diagonals of the square which intersect each other at 90° by the property of square.
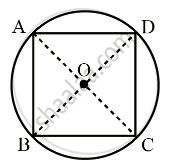
From the above statement, we can see that
∠COD = 90°.
The sum of the angle ∠BOC and ∠OCD is 180° as BD is a straight line.
Hence ∠BOC + ∠OCD = ∠BOD = 180°
∠BOC + 90° = 180°
∠BOC + 180° - 90°
∠BOC = 90°
We can see that the OCB is an isosceles triangle with sides OB and OC of EQual length as they are the radii of the same circle.
In ΔOCB,
∠OBC = ∠OCB ...[Opposite angles to the two equal sides of an isosceles triangle]
Sum of all the angles of a triangle is 180°.
so, ∠OBC + ∠OCB + ∠BOC =180°
∠OBC + ∠OBC + 90° = 180° ...[∠OBC = ∠OCB]
2∠OBC = 180° - 90°
2∠OBC = 90°
2∠OBC = 45°
as ∠OBC = ∠OCB
So, ∠OBC = ∠OCB = 45°
Yes, BD is the diameter of the order.
APPEARS IN
RELATED QUESTIONS
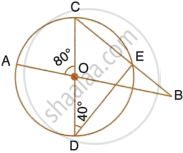
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:
- ∠DCE,
- ∠ABC.
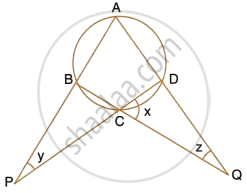
Calculate the angles x, y and z if :
`x/3 = y/4 = z/5`
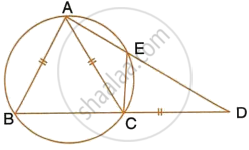
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
- Angle ABC
- Angle BEC
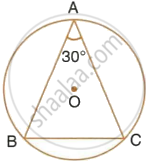
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
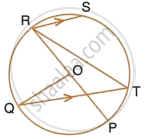
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
- angle QTR
- angle QRP
- angle QRS
- angle STR
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(ii) angle QRP

The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iii) angle QRS
In the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight-sided polygon.
Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC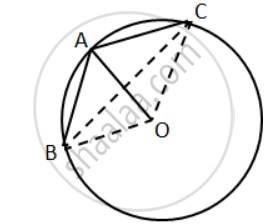
In the given figure, AB = BC = DC and ∠AOB = 50°.
(i) ∠AOC
(ii) ∠AOD
(iii) ∠BOD
(iv) ∠OAC
(v) ∠ODA
In the given figure, AB is a side of regular pentagon and BC is a side of regular hexagon.
(i) ∠AOB
(ii) ∠BOC
(iii) ∠AOC
(iv) ∠OBA
(v) ∠OBC
(vi) ∠ABC
