Advertisements
Advertisements
Question
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.
If ∠MAD = x and ∠BAC = y , Prove that : x = y
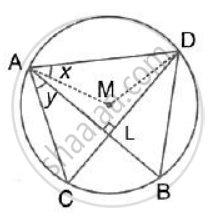
Solution
In the figure, M is the centre of the circle.
Chords AB and CD are perpendicular to each other at L.
∠MAD = x and ∠BAC = y
we have, ∠ABD =90° - y and ∠ABD = 90° - x [proved]
∴ 90° - x 90° - y
⇒ x = y
APPEARS IN
RELATED QUESTIONS
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
A chord of length 8cm is drawn inside a circle of radius 6cm. Find the perpendicular distance of the chord from the centre of the circle.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
OP is the ⊥ bisector of chord AB.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm;
find the length of another chord.
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the center.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.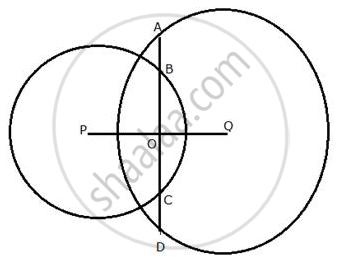
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB. If AB = 32 cm,
find the length of CD.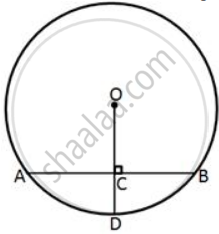
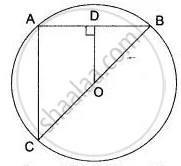
In the given figure, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2 OD.
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.

AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the
(i) radius of the circle
(ii) length of chord CD.
