Advertisements
Advertisements
Question
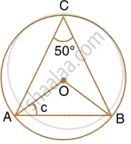
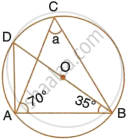
In the following figure, O is the centre of the circle. Find the values of a, b, c and d
Solution

∠AOB = 2∠AOB
= 2 × 50°
= 100°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Also, OA = OB
`=>` ∠OBA = ∠OAB = C
∴ `c = (180^circ - 100^circ)/2 = 40^circ`
APPEARS IN
RELATED QUESTIONS
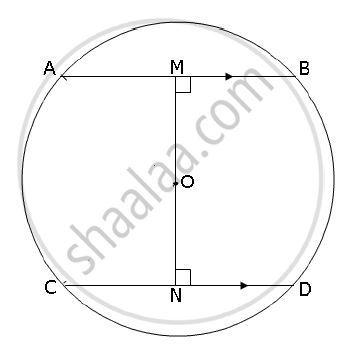
In the figure given below AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
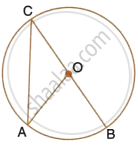
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
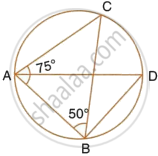
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
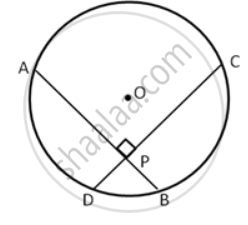
The length of the common chord of two intersecting circles is 30 cm. If the diameters of these two circles are 50 cm and 34 cm, calculate the distance between their centers.
Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP
Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
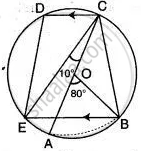
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.