Advertisements
Advertisements
Question
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
Solution
Let AB and CD be two parallel chords of a circle with centre O such that AB = 6 cm and CD = 12 cm.
Let the radius of the circle be r cm,
Draw OP ⊥ AB and OQ ⊥ CD.
Since AB || CD and OP ⊥ AB, OQ ⊥ CD.
Therefore, points O, Q and P are collinear.
Clearly, PQ = 3 cm.
Let OQ = x cm. Then, OP = (x + 3) cm
In right triangles OAP and OCQ, we have
OA2 = OP2 + AP2 and OC2 = OQ2 + CQ2
⇒ r2 = (x + 3)2 + 32 and r2 = x2 + 62

....[ ∵ AP = `1/2"AB" = 3 "cm" and CQ = 1/2"CD = 6 cm`]
⇒ (x + 3)2 + 32 = x2 + 62 ...(On equating the value of r2)
⇒ 6x = 18
⇒ x = 3 cm
Putting the values of x in r2 = x2 + 62, we get
r2 = x2 + 62 = 45
⇒ r = `sqrt45` cm = 6.7 cm
Hence the radius of the circle is 6.7 cm
APPEARS IN
RELATED QUESTIONS
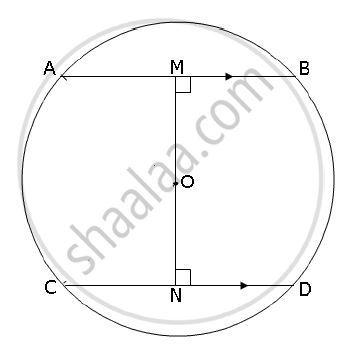
In the figure given below AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
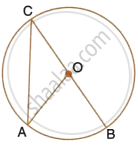
AB and CD are two equal chords of a circle with centre O which intersect each other at right
angle at point P. If OM⊥ AB and ON ⊥ CD; show that OMPN is a square.
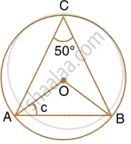
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the values of a, b, c and d
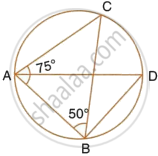
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
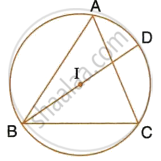
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
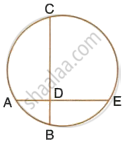
In the figure, chords AE and BC intersect each other at point D. If AD = BD, show that AE = BC.
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP