Advertisements
Advertisements
Question
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
Solution
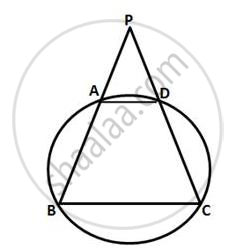
Let ABCD be the given cyclic quadrilateral
Also, PA = PD ...(Given)
∴ ∠PAD = ∠PDA ...(1)
∴ ∠BAD = 180° – ∠PAD
And ∠CDA = 180° – PDA
= 180° – ∠PAD ...(From (1))
We know that the opposite angles of a cyclic quadrilateral are supplementary
∴ ∠ABC = 180° – ∠CDA
= 180° – (180° – ∠PAD)
= ∠PAD
And ∠DCB = 180° – ∠BAD
= 180° – (180° – ∠PAD)
= ∠PAD
∴ ∠ABC = ∠DCB = ∠PAD = ∠PAD
That means AD || BC
APPEARS IN
RELATED QUESTIONS
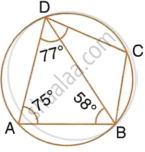
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
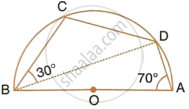
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
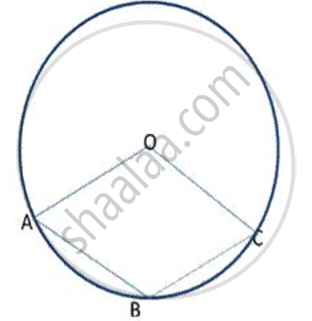
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
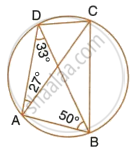
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
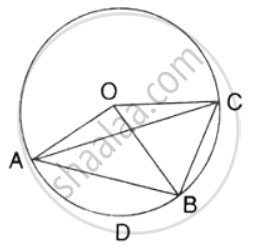
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
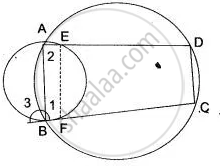
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.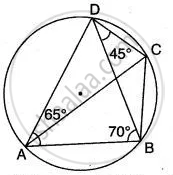
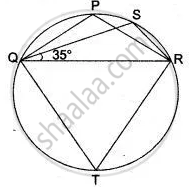
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.