Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
उत्तर
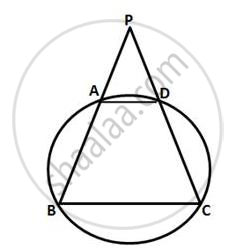
Let ABCD be the given cyclic quadrilateral
Also, PA = PD ...(Given)
∴ ∠PAD = ∠PDA ...(1)
∴ ∠BAD = 180° – ∠PAD
And ∠CDA = 180° – PDA
= 180° – ∠PAD ...(From (1))
We know that the opposite angles of a cyclic quadrilateral are supplementary
∴ ∠ABC = 180° – ∠CDA
= 180° – (180° – ∠PAD)
= ∠PAD
And ∠DCB = 180° – ∠BAD
= 180° – (180° – ∠PAD)
= ∠PAD
∴ ∠ABC = ∠DCB = ∠PAD = ∠PAD
That means AD || BC
APPEARS IN
संबंधित प्रश्न
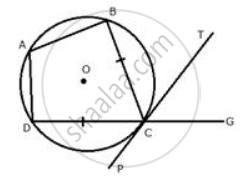
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
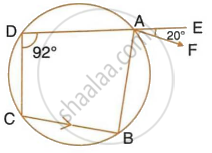
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
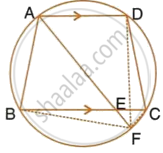
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
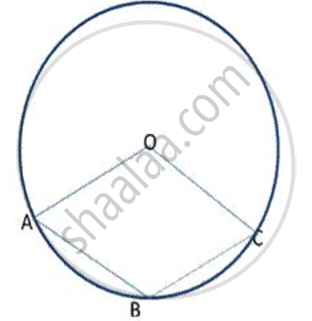
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
