Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

उत्तर

Here ∠ACB = 90°
(Angle in a semicircle is right angle)
Also, ∠ABC = 180° – ∠ADC = 180° – 130° = 50°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
By angle sum property of right triangle ACB,
∠BAC = 90° – ∠ABC = 90° – 50° = 40°
APPEARS IN
संबंधित प्रश्न
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

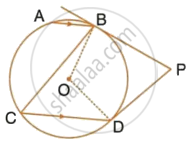
In the given figure, O is the centre of the circle. The tangents at B and D intersect each other at point P. If AB is parallel to CD and ∠ABC = 55°, find:
- ∠BOD
- ∠BPD
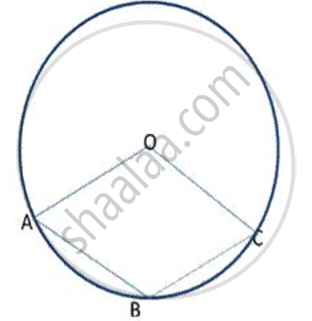
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
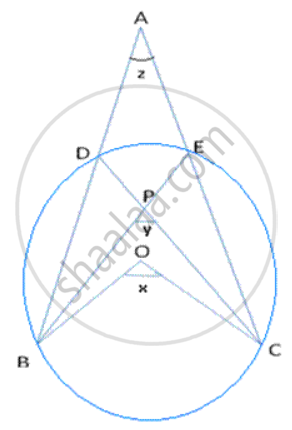
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
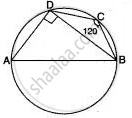
In following fig., O is the centre of the circle. Find ∠ CBD.
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA