Advertisements
Advertisements
Question
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Solution
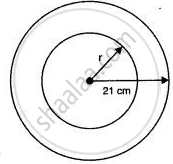
Let the Radius of inner circle be r.
Area between concentric circles = area of outer circle – area of inner circle
⇒ 770 =`22/7`(212 − r2)
⇒ (21)2 − (r2) = `(770 xx 7)/22`
⇒ 212 − r2 = 35 × 7 = 245
⇒ 441 – 245 = r2
⇒ r = `sqrt(196)` = 14 cm
Radius of inner circle = 14 cm.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

In the given figure, if ∠ABC = 45°, then ∠AOC =
The point of concurrence of all angle bisectors of a triangle is called the ______.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
