Advertisements
Advertisements
Question
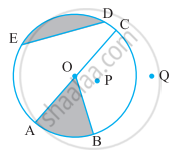
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
Solution
Given: AB = 10 units, AC = 6 units, PC = PQ = x unit.
To find: x
Solution:
Diameter AB = 10 ...[Given]
∴ Radius = `1/2 xx "AB" = 1/2 xx 10` = 5.
∴ OQ = AO = OB = 5 ......(i)
AC = AO + OC .....[A–O–C]
∴ OC = AC – AO
∴ OC = 6 – 5 ......[Given and (i)]
∴ OC = 1 ......(ii)
OQ = OP + PQ ......[O–P–Q]
∴ OP = OQ – PQ
= 5 – x ......(iii) [From (i) and given]
Note that seg AB is tangent to the given smaller circle at point C.
∴ ∠PCO = 90° ......[Tangent theorem]
∴ In ∆PCO,
∠PCO = 90°
∴ OP2 = PC2 + OC2 ......[Pythagoras theorem]
∴ (5 – x)2 = x2 + (1)2 ......[From (ii) and (iii)]
∴ 25 – 10x + x2 = x2 + 1
∴ 10x = 24
∴ x = `24/10` = 2.4
∴ The radius x of the smaller circle is 2.4 units
APPEARS IN
RELATED QUESTIONS
Prove that there is one and only one tangent at any point on the circumference of a circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
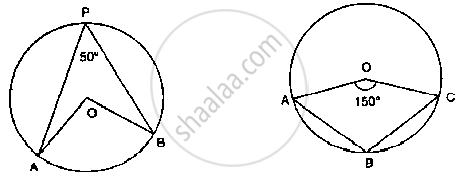
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
From the figure, identify the centre of the circle.