Advertisements
Advertisements
Question
The point of concurrence of all angle bisectors of a triangle is called the ______.
Options
Centroid
Circumcentre
Incentre
Orthocentre
Solution
The point of concurrence of all angle bisectors of a triangle is called the incentre.
APPEARS IN
RELATED QUESTIONS
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
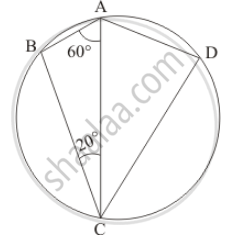
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
Number of circles that can be drawn through three non-collinear points is
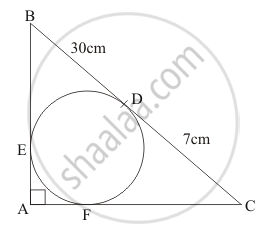
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF
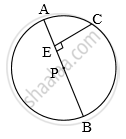
In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
