Advertisements
Advertisements
Question
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
Solution
Let r1 be the radius of the bigger circle and r2 be the radius of the smaller circle.
It is given that the two circles touch each other internally.
∴ Difference between their radii = Distance between the centres of the two circles
⇒ r1 − r2 = 6 cm .....(1)
Also,
Sum of their areas = 116π cm2
\[\therefore \pi {r_1}^2 + \pi {r_2}^2 = 116\pi\]
\[ \Rightarrow {r_1}^2 + {r_2}^2 = 116 . . . . . \left( 2 \right)\]
From (1) and (2), we have
\[\left( r_2 + 6 \right)^2 + {r_2}^2 = 116\]
\[ \Rightarrow {r_2}^2 + 12 r_2 + 36 + {r_2}^2 = 116\]
\[ \Rightarrow 2 {r_2}^2 + 12 r_2 - 80 = 0\]
\[ \Rightarrow {r_2}^2 + 6 r_2 - 40 = 0\]
\[ \Rightarrow {r_2}^2 + 10 r_2 - 4 r_2 - 40 = 0\]
\[ \Rightarrow r_2 \left( r_2 + 10 \right) - 4\left( r_2 + 10 \right) = 0\]
\[ \Rightarrow \left( r_2 + 10 \right)\left( r_2 - 4 \right) = 0\]
\[ \Rightarrow r_2 + 10 = 0 or r_2 - 4 = 0\]
\[ \Rightarrow r_2 = - 10 or r_2 = 4\]
Since the radius of a circle cannot be negative, so r2 = 4 cm.
∴ r1 = r2 + 6 = 4 + 6 = 10 cm
Thus, the radii of the circles are 4 cm and 10 cm.
APPEARS IN
RELATED QUESTIONS
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
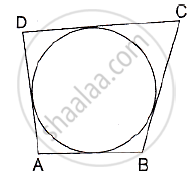
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
A line through the point of contact and passing through centre of the circle is known as ______
