Advertisements
Advertisements
प्रश्न
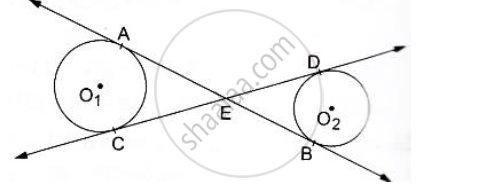
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
उत्तर
We know that tangent segments to a circle from the same external point are congruent.
So, we have
EA = EC for the circle having center O1
and
ED = EB for the circle having center O1
Now, Adding ED on both sides in EA = EC. we get
EA+ ED = EC + ED
⇒ EA + EB = EC + ED
⇒ AB = CD
APPEARS IN
संबंधित प्रश्न
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
The ______________ is the longest chord of a circle
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Is every diameter of a circle also a chord?
