Advertisements
Advertisements
प्रश्न
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?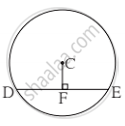
उत्तर
In given figure, seg CF ⊥ Chord DE
∴ DF ≅ DE ......[[A perpendicular drawn from the centre of a circle on its chord bisects the chord]
∴ DF = `1/2` DE
= `1/2 xx 16` .....[Given]
∴ DF = 8 cm
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
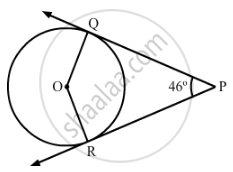
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

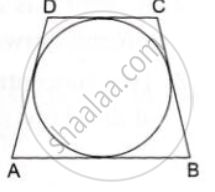
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

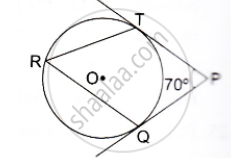
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

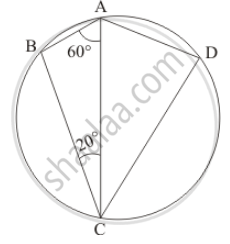
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
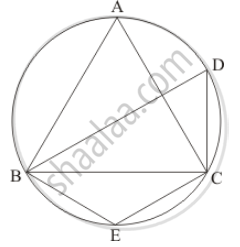
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
In the given figure, if ∠ABC = 45°, then ∠AOC =
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c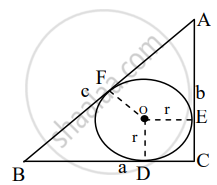
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
From the figure, identify the centre of the circle.
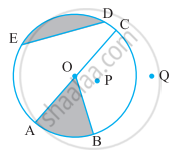
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
