Advertisements
Advertisements
प्रश्न
In the given circle with diameter AB, find the value of x.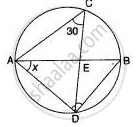
उत्तर
∠ ABD = ∠ ACD = 30° ....(∠s of same segment)
∠ADB = 90° ....(∠ in the semi circle)
In ΔADB,
x° + 90° + 30° = 180° ....(Sum of all ∠s of triangle)
x° = 180° - 120°
x° = 60°.
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
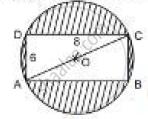
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
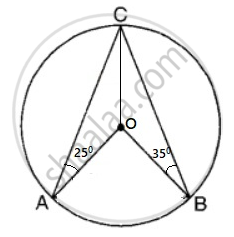
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
