Advertisements
Advertisements
प्रश्न
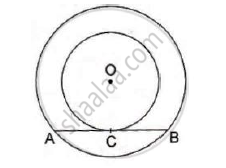
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
उत्तर
Construction: Join OA, OC and OB

We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OCA = ∠OCB = 90°
Now, In Δ OCA and ΔOCB
∠OCA = ∠OCB = 90°
OA = OB (Radii of the larger circle)
OC = OC (Common)
By RHS congruency
Δ OCA ≅ Δ OCB
∴ CA =CB
संबंधित प्रश्न
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
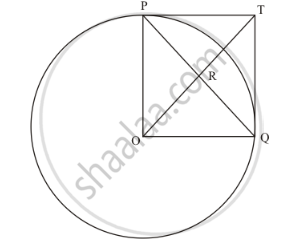
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In the given figure, O is the centre of the circle. Find ∠CBD.

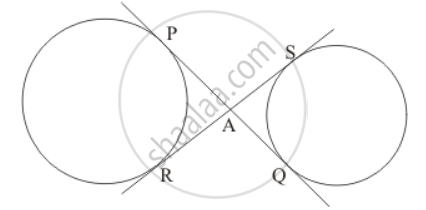
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
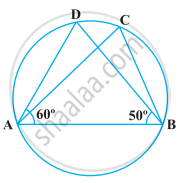
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.