Advertisements
Advertisements
प्रश्न
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
उत्तर
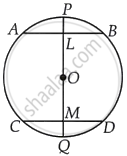
Given: AB and CD are two chords of a circle whose centre is O and PQ is a diameter bisecting the chord AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.
To prove: AB || CD
Proof: Since, L is the mid-point of AB.
∴ OL ⊥ AB ...[Since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]
⇒ ∠ALO = 90° ...(i)
Similarly, OM ⊥ CD
∴ ∠OMD = 90° ...(ii)
From equations (i) and (ii),
∠ALO = ∠OMD = 90°
But, these are alternating angles.
So, AB || CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
true or false
Sector is the region between the chord and its corresponding arc.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In the given figure, O is the centre of the circle. Find ∠CBD.

If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
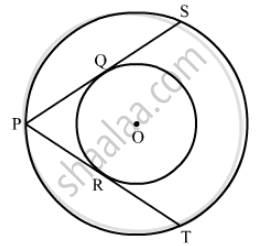
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

In the given figure, O is the centre of the circle. Name all chords of the circle.