Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
рдЙрддреНрддрд░
Given OP = 26 cm
PT = length of tangent = 10cm
radius = OT = ?
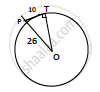
At point of contact, radius and tangent are perpendicular ∠OTP = 90°, ΔOTP is right
angled triangle.
By Pythagoras theorem, ЁЭСВЁЭСГ2 = ЁЭСВЁЭСЗ2 + ЁЭСГЁЭСЗ2
262 = ЁЭСВЁЭСЗ2 + 102
ЁЭСВЁЭСЗЁЭСШ =` (sqrt(676 − 100))`ЁЭСШ
ЁЭСВЁЭСЗ = `sqrt(576)`
= 24 cm
OT = length of tangent = 24 cm
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
From the figure, identify the centre of the circle.
