Advertisements
Advertisements
प्रश्न
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
उत्तर
Given OQ: PQ = 3 : 4
Let OQ = 3x PQ = 4x
OP = y
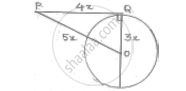
∠OQP = 90° [since at point of contact, tangent is perpendicular to radius]
In ΔOQP, by Pythagoras theorem
𝑂𝑃2 = 𝑂𝑄2 + 𝑄𝑃2
⇒ 𝑦2 = (3𝑥)2 + (4𝑥)2
⇒ 𝑦2 = 9𝑥2 + 16𝑥2 = 25𝑥2
⇒ 𝑦 = `sqrt(25x^2)` = 5𝑥
Perimeter = OQ + PQ + OP = 3x + 4x + 5x = 12x
According to problem perimeter = 60
∴ 12x = 60
x =`60/12`
= 5𝑐𝑚
OQ = 3 × 5 = 15𝑐𝑚
PQ = 4 × 5 = 20 𝑐𝑚
OP = 5 × 5 = 25𝑐𝑚
APPEARS IN
संबंधित प्रश्न
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

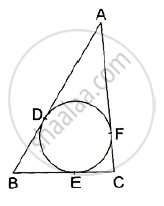
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
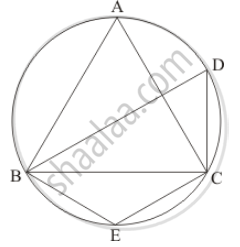
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
Can the length of a chord of a circle be greater than its diameter ? Explain.
Find the radius of the circle
Diameter = 24 cm
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
