Advertisements
Advertisements
प्रश्न
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
उत्तर
Given OQ: PQ = 3 : 4
Let OQ = 3x PQ = 4x
OP = y
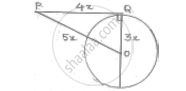
∠OQP = 90° [since at point of contact, tangent is perpendicular to radius]
In ΔOQP, by Pythagoras theorem
𝑂𝑃2 = 𝑂𝑄2 + 𝑄𝑃2
⇒ 𝑦2 = (3𝑥)2 + (4𝑥)2
⇒ 𝑦2 = 9𝑥2 + 16𝑥2 = 25𝑥2
⇒ 𝑦 = `sqrt(25x^2)` = 5𝑥
Perimeter = OQ + PQ + OP = 3x + 4x + 5x = 12x
According to problem perimeter = 60
∴ 12x = 60
x =`60/12`
= 5𝑐𝑚
OQ = 3 × 5 = 15𝑐𝑚
PQ = 4 × 5 = 20 𝑐𝑚
OP = 5 × 5 = 25𝑐𝑚
APPEARS IN
संबंधित प्रश्न
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

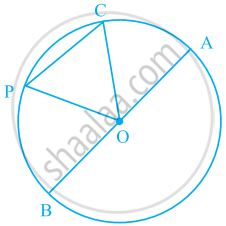
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Draw circle with the radii given below.
2 cm
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
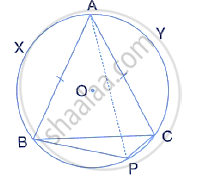
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.