Advertisements
Advertisements
प्रश्न
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर
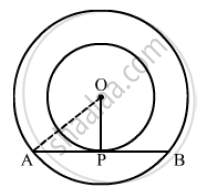
We know that the radius and tangent are perpendicular at their point of contact In right triangle AOP
`AO^2 = OP^2 + PA^2`
⇒ `(6.5) ^2 = (2.5)^2 +PA^2`
⇒`PA^2 = 36`
⇒PA = 6cm
Since, the perpendicular drawn from the center bisects the chord.
∴ PA = PB = 6cm
Now , AB = AP + PB = 6+6 = 12cm
Hence, the length of the chord of the larger circle is 12cm.
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
true or false
A circle is a plane figure.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
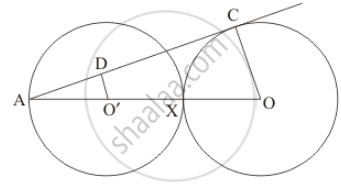
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
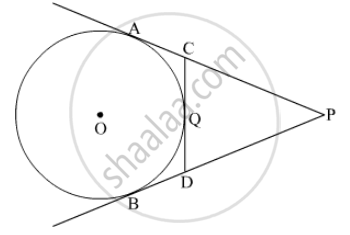
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c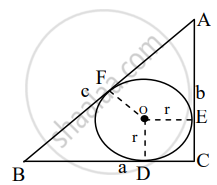
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
From the figure, identify a segment.

