Advertisements
Advertisements
प्रश्न
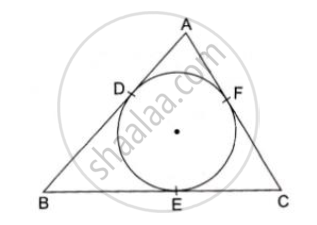
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
उत्तर
Sol:
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
AD = AF, BD = BE and CE = CF
Now, AD + BD = l2cm …….(1)
AF + FC = l0 cm
⇒ AD + FC = l0 cm …….(2)
BE + EC = 8 cm
⇒ BD + FC = 8cm …….(3)
Adding all these we get
AD + BD + AD + FC + BD + FC = 30
⇒ 2(AD + BD + FC) = 30
⇒ AD + BD + FC = l5cm …….(4)
Solving (1) and (4), we get
FC = 3 cm
Solving (2) and (4), we get
BD = 5 cm
Solving (3) and (4), we get
and AD = 7 cm
∴ AD = AF =7 cm, BD = BE = 5 cm and CE = CF =3 cm
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
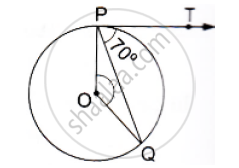
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
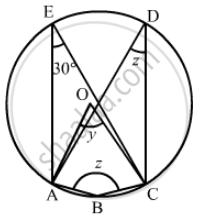
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
Find the radius of the circle
Diameter = 24 cm
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
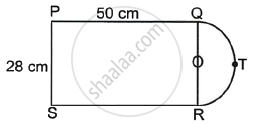
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.