Advertisements
Advertisements
प्रश्न
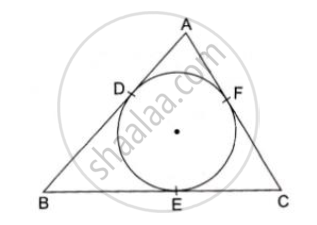
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
उत्तर
Sol:
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
AD = AF, BD = BE and CE = CF
Now, AD + BD = l2cm …….(1)
AF + FC = l0 cm
⇒ AD + FC = l0 cm …….(2)
BE + EC = 8 cm
⇒ BD + FC = 8cm …….(3)
Adding all these we get
AD + BD + AD + FC + BD + FC = 30
⇒ 2(AD + BD + FC) = 30
⇒ AD + BD + FC = l5cm …….(4)
Solving (1) and (4), we get
FC = 3 cm
Solving (2) and (4), we get
BD = 5 cm
Solving (3) and (4), we get
and AD = 7 cm
∴ AD = AF =7 cm, BD = BE = 5 cm and CE = CF =3 cm
APPEARS IN
संबंधित प्रश्न
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

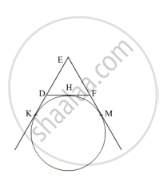
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
The longest chord of a circle is __________
Find the diameter of the circle
Radius = 10 cm
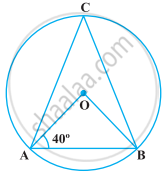
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

From the figure, identify three radii.