Advertisements
Advertisements
प्रश्न
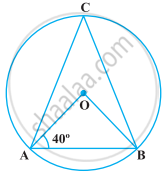
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
पर्याय
50º
40º
60º
70°
उत्तर
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to 50º.
Explanation:

Given: ∠OAB = 40º
Now, in triangle OAB,
OA = OB ...[Radii of circle]
So, ∠OAB = ∠OBA = 40º ...[Angle opposite to equal sides are equal]
So, ∠AOB = 180º – (40º + 40º) = 100º
As we know that angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
So, ∠ACB = `1/2` ∠AOB = `1/2 xx 100^circ` = 50º
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

The length of tangent from an external point on a circle is always greater than the radius of the circle.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
From the figure, identify two points in the interior.

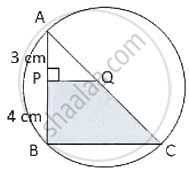
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.