Advertisements
Advertisements
प्रश्न
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
उत्तर
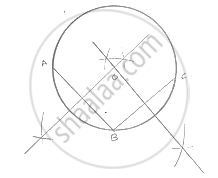
Steps of constructions:
(1) Take three point A, B and C the given circle
(2) Join AB and BC
(3) Draw the perpendicular bisectors of chord AB and BC which intersect each other at O.
(4) Point O will be the required center of the circle because we know that the perpendicular
bisector of the cord always passes through the center
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
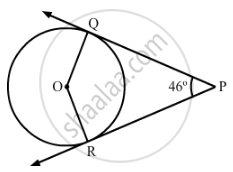
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

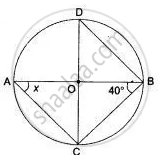
If O is the centre of the circle, find the value of x in each of the following figures
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

