Advertisements
Advertisements
प्रश्न
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

उत्तर
In the given figure,
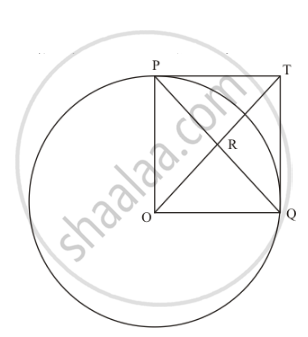
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal) Now considering the angles of the quadrilateral PTQO, we have,
`∠POQ=90^o` (Given in the problem)
`∠OPT=90^o` (The radius of the circle will be perpendicular to the tangent at the point of contact)
`∠ TQO=90^o` (The radius of the circle will be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠ POQ+∠TQO+∠OPT+∠PTQ=360^o`
`90^O+90^O+90^O+∠ PTQ=360^o`
`∠ PTQ=90^o`
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
संबंधित प्रश्न
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.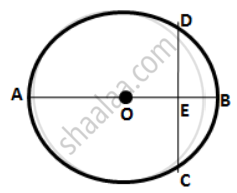
Find the radius of the circle
Diameter = 24 cm
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
What is the area of a semi-circle of diameter ‘d’?
