Advertisements
Advertisements
प्रश्न
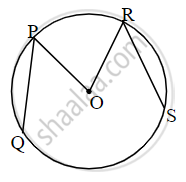
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
उत्तर
(i) m(arc PR) = m∠POR ...[Definition of measure of arc]
∴ m(arc PR) = 70°
(ii)
chord PQ ≅ chord RS .....[Given]
∴ m(arc PQ) = m(arc RS) = 80° .....[Corresponding arcs of congruent chords of a circle are congruent]
Now,
m(arc QS) + m(arc PQ) + m(arc PR) + m(arc RS) = 360° ...[Measure of a circle is 360°]
∴ m(arc QS) + 80° + 70° + 80° = 360°
∴ m(arc QS) + 230° = 360°
∴ m(arc QS) = 130°
(iii) m(arc QSR) = m(arc QS) + m(arc SR) = 130° + 80° ...[Arc addition property]
m(arc QSR) = 210°
APPEARS IN
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c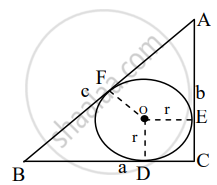
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
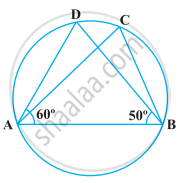
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Is every chord of a circle also a diameter?
