Advertisements
Advertisements
प्रश्न
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
पर्याय
30°
60°
90°
120°
उत्तर
120°
We are given that an equilateral ΔABC is inscribed in a circle with centre O. We need to find ∠BOC
We have the following corresponding figure:

We are given AB = BC = AC
Since the sides AB, BC, and AC are these equal chords of the circle.
So, the angle subtended by these chords at the centre will be equal.
Hence
`angleAOB + angleBOC + angleAOC = 360`
`angleBOC + angleBOC + angleBOC = 360`
`3angleBOC = 360`
`angleBOC = 360/3`
`angleBOC = 120°`
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Fill in the blank
A continuous piece of a circle is ............... of the circle
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

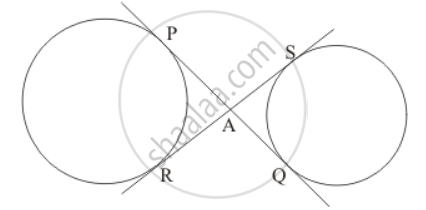
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

The radius of a circle of diameter 24 cm is _______
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

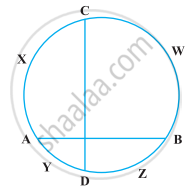
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.